Difference between revisions of "Introduction to Detection of Gamma Radiation"
Jonpo@uio.no (talk | contribs) (→Excited States) |
Jonpo@uio.no (talk | contribs) (→Excited States) |
||
| Line 3: | Line 3: | ||
<br> | <br> | ||
| − | ==== Excited States<br> | + | ==== Excited States<br> ==== |
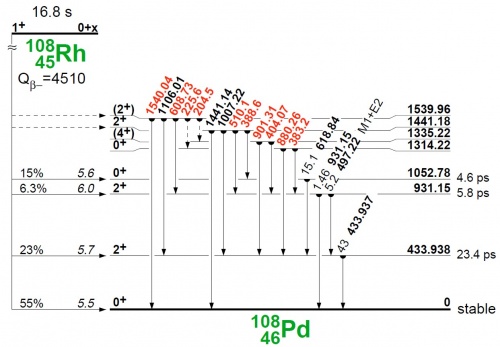
| − | When a nucleus decays by emitting an alpha or beta particle the daughter product will frequently be in an excited state. The excess energy (related to the daughter's ground state) is usually released as gamma radiation. The deexitation of such excited states does not always occur directly to the ground state, but can go via lower-lying excited states. Frequently the deexcitation scheme can be quite comples, as illustrated in the figure (copied from Table of Isotopes, eight edition) | + | When a nucleus decays by emitting an alpha or beta particle the daughter product will frequently be in an excited state. The excess energy (related to the daughter's ground state) is usually released as gamma radiation. The deexitation of such excited states does not always occur directly to the ground state, but can go via lower-lying excited states. Frequently the deexcitation scheme can be quite comples, as illustrated in the figure (copied from Table of Isotopes, eight edition) |
| − | |||
| + | [[Image:108Rh_beta_disintegration.jpg|500px]] | ||
| + | <br> | ||
| − | *Emission of electromagnetic radiation (gamma rays). The energy of a gamma lies between 10 keV and 104 MeV, given by E = hv<br> | + | <br> |
| − | *Transfer of the excitation energy to an electron, where the electron is called a conversion electron.<br> | + | |
| + | *Emission of electromagnetic radiation (gamma rays). The energy of a gamma lies between 10 keV and 104 MeV, given by E = hv<br> | ||
| + | *Transfer of the excitation energy to an electron, where the electron is called a conversion electron.<br> | ||
*Absorption of photons in matter<br> | *Absorption of photons in matter<br> | ||
| − | A photon can interact with matter in three different ways. <br> | + | A photon can interact with matter in three different ways. <br> |
| − | #The first way is called the photoelectric effect, where the gamma energy is transferred in its entirety to an electron in one of the inner shells of an atom or ion in the absorption material. The electron emitted has a kinetic energy corresponding to the gamma energy minus the binding energy of the electron. The electron velocity decreases via electrostatic interactions with absorbator electrons and protons, and thus gives off its kinetic energy to the absorber. <br> | + | #The first way is called the photoelectric effect, where the gamma energy is transferred in its entirety to an electron in one of the inner shells of an atom or ion in the absorption material. The electron emitted has a kinetic energy corresponding to the gamma energy minus the binding energy of the electron. The electron velocity decreases via electrostatic interactions with absorbator electrons and protons, and thus gives off its kinetic energy to the absorber. <br> |
| − | #The second way a photon can interact with matter is called Compton scatter. Parts of the gamma energy is emitted to an (unbound) electron and this electron energy is deposited in the absorber (Compton electron). The loss of energy from the photons interaction increases its wavelength, and therby changes its direction. The scattered gamma can either leave the absorber or interact again. If a gamma quant from Compton scattering reacts again, it will happen so quickly that it would be impossible to observe each of the two steps. <br> | + | #The second way a photon can interact with matter is called Compton scatter. Parts of the gamma energy is emitted to an (unbound) electron and this electron energy is deposited in the absorber (Compton electron). The loss of energy from the photons interaction increases its wavelength, and therby changes its direction. The scattered gamma can either leave the absorber or interact again. If a gamma quant from Compton scattering reacts again, it will happen so quickly that it would be impossible to observe each of the two steps. <br> |
#Pair formation is the third way of interaction. When a photon has higher energy than 1022 MeV an electron/positron pair may spontaneously form. The total kinetic energy of the two elementary particles are equal to the energy of the gamma minus 1022 MeV. The electron vil transfer its energy as described under the last part of 1. As the positron is slowed down the chance it will interact with an electron increases before it eventually does and both particles disappear and turns into 2 quants of 511 keV, called anhiliation energy. <br> | #Pair formation is the third way of interaction. When a photon has higher energy than 1022 MeV an electron/positron pair may spontaneously form. The total kinetic energy of the two elementary particles are equal to the energy of the gamma minus 1022 MeV. The electron vil transfer its energy as described under the last part of 1. As the positron is slowed down the chance it will interact with an electron increases before it eventually does and both particles disappear and turns into 2 quants of 511 keV, called anhiliation energy. <br> | ||
| − | <br> | + | <br> |
The intensisity of a monoenergetic gamma ray decreases exponentially in matter, according to the following equation: | The intensisity of a monoenergetic gamma ray decreases exponentially in matter, according to the following equation: | ||
| Line 32: | Line 35: | ||
<math>d_{1/2} = \frac{ln2}{\mu}</math> | <math>d_{1/2} = \frac{ln2}{\mu}</math> | ||
| − | <br> <br> | + | <br><br> |
[[Category:Radiation_protection]] | [[Category:Radiation_protection]] | ||
Revision as of 12:32, 14 October 2012
Return to Main
Excited States
When a nucleus decays by emitting an alpha or beta particle the daughter product will frequently be in an excited state. The excess energy (related to the daughter's ground state) is usually released as gamma radiation. The deexitation of such excited states does not always occur directly to the ground state, but can go via lower-lying excited states. Frequently the deexcitation scheme can be quite comples, as illustrated in the figure (copied from Table of Isotopes, eight edition)
- Emission of electromagnetic radiation (gamma rays). The energy of a gamma lies between 10 keV and 104 MeV, given by E = hv
- Transfer of the excitation energy to an electron, where the electron is called a conversion electron.
- Absorption of photons in matter
A photon can interact with matter in three different ways.
- The first way is called the photoelectric effect, where the gamma energy is transferred in its entirety to an electron in one of the inner shells of an atom or ion in the absorption material. The electron emitted has a kinetic energy corresponding to the gamma energy minus the binding energy of the electron. The electron velocity decreases via electrostatic interactions with absorbator electrons and protons, and thus gives off its kinetic energy to the absorber.
- The second way a photon can interact with matter is called Compton scatter. Parts of the gamma energy is emitted to an (unbound) electron and this electron energy is deposited in the absorber (Compton electron). The loss of energy from the photons interaction increases its wavelength, and therby changes its direction. The scattered gamma can either leave the absorber or interact again. If a gamma quant from Compton scattering reacts again, it will happen so quickly that it would be impossible to observe each of the two steps.
- Pair formation is the third way of interaction. When a photon has higher energy than 1022 MeV an electron/positron pair may spontaneously form. The total kinetic energy of the two elementary particles are equal to the energy of the gamma minus 1022 MeV. The electron vil transfer its energy as described under the last part of 1. As the positron is slowed down the chance it will interact with an electron increases before it eventually does and both particles disappear and turns into 2 quants of 511 keV, called anhiliation energy.
The intensisity of a monoenergetic gamma ray decreases exponentially in matter, according to the following equation:
I = I0e - μx
where μ is the absorption coeffecient and x is the thickness of the absorbator.
If we set into the above equation, we get the following: