Difference between revisions of "KJM-FYS 5920 Lab Exercise 2 - Student Report"
(→Detector Performance) |
(→Detector Performance) |
||
| Line 112: | Line 112: | ||
<math>F = \frac{\Delta E ^2}{2.35^2 \cdot E \cdot w} </math> | <math>F = \frac{\Delta E ^2}{2.35^2 \cdot E \cdot w} </math> | ||
| − | + | Inserting the values into this equation gives us an experimental value of the Fano factor | |
| − | Inserting values into | ||
<math>F = \frac{\left ( 1.26 \cdot 10^3 \right ) ^2}{2.35^2 \cdot \left ( 662\cdot 10^3 \right ) \cdot 2.96} = 0.1467 \approx 0.15 </math> | <math>F = \frac{\left ( 1.26 \cdot 10^3 \right ) ^2}{2.35^2 \cdot \left ( 662\cdot 10^3 \right ) \cdot 2.96} = 0.1467 \approx 0.15 </math> | ||
Revision as of 17:17, 14 October 2010
KJM-FYS 5920 Lab Exercise 2 report (Autumn 2010):
Contents
Setting up a HPGe gamma-spectroscopy system
Participating students (authors): Tomas Kvalheim Eriksen, Alexander Mauring, Therese Renstrøm, Inger Eli Ruud, Pejman Mansouri Samani, Martin Ytre-Eide, Sindre Øvergaard.
Teachers: Prof. Jon Petter Omtvedt and Hilde-Therese Nyhus (lab assistant)
University of Oslo 1st October 2010
Introduction
(Written by: Jon Petter Omtvedt)
Detector and Preamplifier Signals
(Written by: Pejman)
Spectroscopy Amplifier Setup & Signals
(Written by: Martin)
ADC and MCA Setup
ADC (or A/D) means analog to digital converter. The ADC is a fundamental link between analog and digital electronics as it converts information in an analog signal to an equivalent digital form. This happens by the ADC accepting input pulses of 0-10V and converting these to digital numbers ranging from 0-8195. (The ranges here are from the device used in the experiment, the voltage- and digital number range may differ from model to model.) E.g for this device an input pulse of 2.0V would be converted to the digital number 1639.
MCA means multi-channel analyzer. Together with the ADC it forms a unit which sorts out and keeps count of the different pulses, and stores the count of each pulse in a multi-channel memory. The memory channel adress corresponds to the digitized value of the signal. In this way the pulses received from the detector system are sorted out and counted according to pulse height (voltage), which is proportional to the gamma energy. The total number of channels into which the voltage range is digitized is known as the conversion gain, and it determines the resolution of the MCA.
It can be connected to a computer, or another output device, in order to view the acquired spectre (Counts per channel).
The SA is connected to the ADC/MCA for conversion of the enhanced pulses. The next step is to adjust the gain, we want 0.5keV per channel. 137Cs has a gamma peak at 662keV, this energy then corresponds to channel number 1324. What voltage should the incoming pulses have? The answer is channel number divided by total channel number times the maximum voltage in the range of the ADC, here (1324/8195)*10V=1.62V.
With 137-Cs in front of the detector, we adjust the gain until we see pulses about 1.62V on the oscilloscope. The gain is then 10.348 and the MCA should now have a resolution of 0.5keV per channel.
Now the ADC/MCA unit is ready for connection to a computer to view the acquired spectre, and for further calibration.
(Written by: Tomas)
Calibration
The electrical signal from the Ge-detector has now propagated through many components that has both shaped and enhanced the pulse. The energy of interest is of course that deposited by the gamma in the detector. The Gaussian-like pulse produced in the main amplifier will have an amplitude proportional to the gamma-energy. The signals from the main amplifier are analysed by the ADC/MCA unit. Information from the MCA is received by the lab-computer in the form of a histogram; number of counts pr energy bin. We use the spectrum analysis program MAESTRO to look at the resulting spectra. Since the detector has an approximately linear response, we have that:
E_gamma = a * channel nr + b, where we ignore higher order terms.
To determine the two unknowns, a and b, we need two equations. We need two known gamma energies and their corresponding channel number. Co-60 has two prominent peaks, one at 1173 keV and one at 1332 keV. Using the peak-finding function in MAESTRO, we find the channel number of the two peaks. The radioactive isotope Co-60 provides excellent calibration for energies in the region between 1-1.5 MeV. We recognize that the energy separation between the two peaks; delta_E = (1332 - 1173) keV = 159 keV, is small compared to the uncertainties connected to determination of peaks and detector resolution. A small error in the determination of a and b will give a large mistake for energies far from the calibration region (1173 - 1332 keV).
In the spectrum of Co-60 we observed three strong peaks in the interval between 1 and 1.5 MeV, but we expected only two . The unknown peak appeared to come from the considerable concentration of K-40 in the concrete walls of the lab. Table of Isotopes gives one gamma energy for K-40, E_gamma = 1460 keV. This peak would correspond to the highest of the three detected peaks. We also tested this theory by removing the Co-60 source from in front of the Ge-detector. The two peaks with the lower energy disappeared as expected. The reason why the background line was so strong, was that we did not shield the source with lead blocks. A rough calibration was performed with Co-60 giving poor results for low energy gammas.
We need an additional calibration-point at lower energy to get a more accurate calibration for low gamma energies. Co-57 has clear, separable peak at E_gamma = 122 keV. We finally decided to use the 122 keV peak from Co-57 and the 1332 keV peak from Co-60 as calibration points. The energy-separation between these peaks are: delta_E = (1332-122)keV = 1210 keV. These points certainly gave a better calibration for lower energy gammas and still good results for higher energies.
Still the spectrum showing in MAESTRO needed improvements. E_gamma = 0 keV should correspond to channel nr 0. But in our case we had a negative energy in channel 0. We tuned the ADC until we got it right. New calibration was performed whenever we changed voltage. We also noticed that the energy pr bin was a bit over the pre set width of 0.5 keV. Increasing the amplification decreased the width of the bins to ca 0.5 keV.
At this point in the experiment we were ready to look at spectra in MAESTRO and seeing correct energies of the peaks.
(Written by: Therese and Inger Eli )
Detector Performance
(Written by: Alexander and Sindre)
Introduction and theory
An important factor for detectors which are designed to measure energy spectra of gamma radiation is the energy resolution, R, given as ΔE/E. Energy resolution describes to which extent the detector can distinguish between two close lying energy peaks. It is usually given in terms of the full with at half maximum (FWHM) of the peak rather than in terms of standard deviation. Assuming Gaussian shaped peaks, the general relation between standard deviation σ and FWHM is given by
ΔE = FWHM = 2.35σ
Peaks which are closer in energy than one FWHM interval are usually considered un-resolvable. The two dominant contributions to the resolution are from the detector itself and from the electronics, so the total peak resolution can be expressed as
For semiconductor detectors, the standard deviation due to counting statistics related to the charge production in the detector following the absorption of a gamma photon is given by
Where J is the mean number of electron-hole pairs created for a specific energy, and F is the Fano factor which will be described in detail later. The relative detector resolution can then be expressed as
In the last expression, w is the mean energy required to create an electron-hole pair (2.96 eV for Germanium), and E is the energy deposited in the Ge crystal.
In this part of the exercise we experimentally determine the Fano factor. Using a pulse generator to eliminate the detector resolution we can measure the electronics resolution directly, thereby isolating the individual contributions from the detector and the electronics. The data obtained allowed us to calculate the resolution from the detector itself and furthermore calculate the Fano factor. The Fano factor is a function of all the various fundamental processes which can lead to an energy transfer in the detector. It is difficult to calculate the Fano factor theoretically, but it is possible to determine it experimentally.
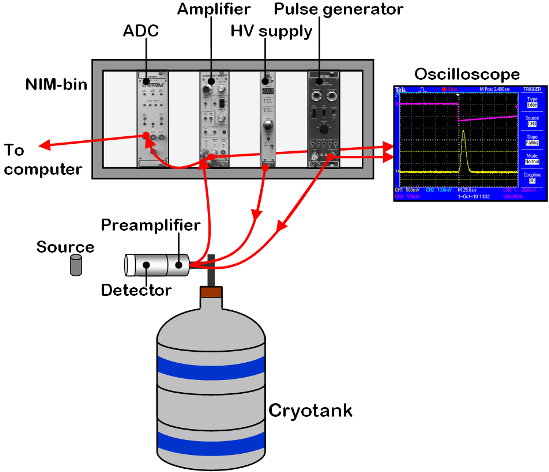
Experimental setup and results
The above figure shows the experimental setup used for this part of the exercise. The 662 keV line from a radioactive Cs-137 source was used to measure the total FWHM. The result was FWHM = ΔE = 2.22 keV. In order to measure the contribution to the FWHM from the associated electronics the radioactive source was replaced by a produced signal from a pulse generator at 673 keV. The resulting FWHM was = 1.83 keV. The contribution from the detector is then
Knowing that the energy resolution is given as ΔE/E we can write
Solving this equation for F yields
Inserting the values into this equation gives us an experimental value of the Fano factor
The nominal value of F is 0.13 which means the experiment gave us a decent estimate of the Fano factor for Germanium.
Conclusions
Conclusion
(Written by: )